46. Функции хэширования. Требования предъявляемые к функциям хэширования.     Ключевые функции хэширования. Безключевые функции хэширования.

Введение

Для решения задач обеспечения целостности наблюдаемости и подлинности информации применяются криптографические контрольные суммы. Методы формирования криптографических контрольных сумм можно разделить на два класса: на базе симметричных криптографических преобразований (коды аутентификации сообщений (КАС)) и использующие несимметричные преобразования (цифровые подписи) с применением секретных ключей. Такие функции могут применяться как непосредственно в качестве криптографической контрольной суммы, так и в других преобразованиях. Например, для формирования цифровой подписи необходима эффективная функция отображения сообщения в образ небольшой фиксированной длины (хэш-значение, хэш-код или просто хэш). Эти функции называют функциями хэширования или хэш-функциями.

1.       Классификация функций хэширования

Функцией хэширования (в широком смысле) называется функция , удовлетворяющая минимум двум требованиям [1]:

1.        Сжатие – функция  отображает входное сообщение  произвольной конечной длины в хэш-значение  небольшой фиксированной длины, при этом входное сообщение будем называть прообразом.

2.        Простота вычисления – для заданной функции  и сообщения , вычисляется не выше чем с полиномиальной сложностью.

Все существующие функции хэширования можно разделить на два больших класса: бесключевые хэш-функции, зависящие только от сообщения, и хэш-функции с секретным ключом, зависящие как от сообщения, так и от секретного ключа.

Подклассом бесключевых хэш-функций являются коды обнаружения изменений (modification detection codes, MDC-коды). В криптографии применяются специфические подклассы MDC-кодов, являющиеся однонаправленными и бесколлизионными хэш-функциями, которые получили широкое распространение в системах цифровой подписи.

Функции выработки кодов аутентификации сообщений (КАС) являются подклассом ключевых хэш-функций и обладают дополнительным свойством вычислительной стойкости.

По используемым внутренним преобразованиям функции хэширования можно разделить на:

·         функции, использующие битовые логические преобразования. Эти функции применяют к входному сообщению побитовые нелинейные операции “И”, “ИЛИ”, “НЕ”, “ИСКЛЮЧАЮЩЕЕ ИЛИ”, различные сдвиги и, как правило, являются многоцикловыми;

·         функции, использующие блочные симметричные шифры. Используются в основном для реализации функций выработки КАС;

·         функции, использующие преобразования в группах, полях и кольцах с целочисленным или полиномиальным базисом;

·         функции, использующие матричные преобразования.

Ключевые функции хеширования

В криптографических приложениях к ключевым функци­ям хеширования предъявляются следующие основные требо­вания:

— невозможность фабрикации;

— невозможность модификации.

Первое требование означает высокую сложность подбора сообщения с правильным значением свертки. Второе — высо­кую сложность подбора для заданного сообщения с извест­ным значением свертки другого сообщения с правильным значением свертки.

Иногда эти свойства объединяют в одно более сильное свойство — свойство вычислительной устойчивости. Это требование означает высокую сложность подбора для задан­ного множества сообщений(быть может, пустого) с известными значениями сверток еще одного сообщения х,  , с правильным значением свертки (возмо­жен случай).

Ключевые функции применяются в ситуациях, когда сто­роны доверяют друг другу и могут иметь общий секретный ключ. Обычно в этих условиях не требуется, чтобы система обеспечивала защиту в случае отказа получателя от факта по­лучения сообщения или его подмены. Поэтому от ключевых хеш-функций не требуется устойчивости к коллизиям.

Обычные атаки на ключевые хеш-функции заключаются в имитации, то есть в передаче сфабрикованных сообщений в пустом канале, а также в подмене передаваемых сообщений с целью навязывания приемной стороне ложных сообщений.

Заметим, что из свойства вычислительной устойчивости вытекает невозможность определения ключа, используемого хеш-функцией, так как знание ключа дает возможность вы­числять значение свертки для любого набора данных. В то же время обратное утверждение неверно, так как подбор значе­ния функции хеширования возможен в некоторых случаях без предварительного определения ключа.

В качестве примера рассмотрим широко распространен­ную хеш-функцию, построенную на основе одношаговой сжимающей функции вида

где— алгоритм блочного шифрования.

Для вычисления значения h(M) сообщение Μ представ­ляется в виде последовательности n-битовых блоков  . Если при этом длина сообщения не кратна длине блока, то последний блок неким специальным образом допол­няется до полного блока. Алгоритм вычисления свертки име­ет следующий вид:

 (2)

Такой режим в ГОСТе 28147-89 называется режимом выработки имитовставки.

В случае когда ключ добавляется в конец сообщения со­гласно формуле , знание коллизии для функции   h,   то   есть   пары ,   такой,   что

 , позволяет вычислять значения  для любого ключа к. Поэтому трудоемкость моди­фикации сообщенияоценивается не величиной а сравнима с трудоемкостью поиска коллизии, оцениваемой величиной, так как в данном случае применима атака, основанная на парадоксе "дней рождений".

В связи с этим более предпочтительными являются спо­собы введения ключа, при которых ключ вставляется в сооб­щение не один, а, по крайней мере, два раза. Два таких способа:

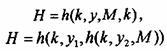
где— дополнения ключа к до размера, кратного

длине блока п. Для определенных бесключевых хеш-функций h такой подход позволяет строить эффективно вычислимые и устойчивые к атакам ключевые хеш-функции. Недостатком такого метода является слишком большая длина η свертки. Дело в том, что для целей проверки целостности обычно вы­бирают длину свертки n в пределах 32-64, а для аутентифи­кации необходимо условие

Бесключевые функции хеширования

Обычно требуется, чтобы бесключевые хеш-функции об­ладали следующими свойствами:

1) однонаправленность,

2) устойчивость к коллизиям,

3) устойчивость к нахождению второго прообраза, означающими соответственно высокую сложность нахожде­ния сообщения с заданным значением свертки; пары сообще­ний с одинаковыми значениями свертки; второго сообщения с тем же значением свертки для заданного сообщения с извест­ным значением свертки.

Например, хеш-функция CRC-32, представляющая собой контрольную сумму, является линейным отображением и по­этому не удовлетворяет ни одному из этих трех свойств.

Для построения примера хеш-функции, удовлетворяющей свойству   1),   рассмотрим   функцию,   заданную   формулой  — алгоритм блочного шифрования. Такая функция является однонаправленной по обоим аргу­ментам. Поэтому на ее основе можно построить хеш-функцию по правилу (1), определив одношаговую сжимаю­щую функцию одной из следующих формул:

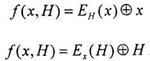
Первая из этих функций лежит в основе российского стандарта хеш-функции, а вторая — в основе американского стандарта SHA.

Справедливо следующее

Утверждение 1. Если функция хеширования h построена на основе одношаговой сжимающей функции f по правилу (1), то из устойчивости к коллизиям функции f следует устойчи­вость к коллизиям функции h.

[Действительно, если у функции h имеется коллизия, то на некотором шаге i должна существовать коллизия у функции f (при определении коллизий функцию следует рассматривать как функцию от одного переменного, полученного конкатенацией переменныхв один входной вектор)].

Укажем взаимозависимость между свойствами 1) и 2).

Утверждение 2. Если хеш-функция устойчива к коллизи­ям, то она устойчива к нахождению второго прообраза.

[Действительно, если для заданной пары сообщение-свертка можно подобрать второй прообраз, то полученная пара сообщений будет составлять коллизию.]

Утверждение 3. Устойчивая к коллизиям хеш-функция не обязана быть однонаправленной.

В качестве примера несжимающей функции приведем функцию h(x) = χ, которая, очевидно,  является устойчивой к коллизиям и к нахождению второго прообраза, но не явля­ется однонаправленной.

В качестве примера сжимающей хеш-функции рассмот­рим функцию h, определенную условиями

h(x) = (1, χ) , если битовая длина χ равна п,

h(x) = (0, g(x)), если битовая длина χ больше п,

где g(x) — сжимающая n-битовая функция, устойчивая к кол­лизиям. Функция h также является устойчивой к коллизиям и к нахождению второго прообраза, но, очевидно, не является однонаправленной.

Утверждение 4.   Пусть  — хеш-функция и

 . Тогда если существует эффективный алгоритм обращения функции h, то существует вероятностный алго­ритм нахождения коллизии функции h с вероятностью успе­ха, большей 1/2.

Доказательство. Будем случайно и равновероятно вы­бирать сообщение х, вычислять и срав­нивать. Покажем, что данный алгоритм имеет вероят­ность успеха. Под успехом мы понимаем построение  , отличного от х

Пусть — разбиение X на классы, состоящие из сообщений с одинаковыми значениями хеш-функции. Ясно, что . Легко заметить, что выполняют­ся следующие соотношения:

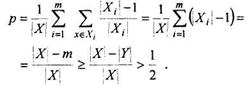
Утверждение доказано.

Заметим, что трудоемкость подбора прообраза для одно­направленной  функции  или трудоемкость  поиска  второго прообраза оцениваются    величиной. В то же время трудоемкость поиска коллизии оценивается величиной  , так как в данной ситуации применима атака, осно­ванная на парадоксе "дней рождений".

Рассмотрим конкретные примеры хеш-функций, постро­енных на основе некоторых алгоритмов преобразования бло­ков.

Пусть— алгоритм блочного шифрования, n — размер блока, l — размер ключа, и G — некоторое отображение, ста­вящее в соответствие вектору длины η вектор длины l.

Примеры бесключевых хеш-функций дают из­вестные алгоритмы MD-4, MD-5 и SHA. Они оперируют с блоками длины и, совпадающей с длиной результирующего значения свертки, причем η = 128 для алгоритма MD-4, и η = = 160 для MD-5 и SHA. Указанные алгоритмы спроектирова­ны специально с учетом эффективной реализации на 32-разрядных ЭВМ.

При их использовании исходное сообщение Μ разбивает­ся на блоки длиной т = 512 бит. Последний блок формирует­ся путем дописывания к концу сообщения комбинации  до получения блока размера 448 бит, к которому затем добав­ляется комбинация из 64 бит, представляющая битовую длину сообщения. Затем вычисляется значение свертки согласно процедуре (1) с использованием одношаговой сжимающей функции, заданной формулой где χ —блок сообщения длины т = 512 бит, Η— блок из η бит, а Е_х — некоторое преобразование множества блоков. Значение начального вектора определяется в описании преобразования Е_х.

В стандарте хеш-функции ГОСТ Ρ 34.11-94 приняты зна­чения n = т — 512. Одношаговая сжимающая функция f(x, Η), используемая для вычисления последовательности

значений, построена на базе четырех параллельно работающих схем блочного шифрования (ГОСТ 28147-89), каждая из которых имеет 256-битовый ключ и оперирует с блоками размера 64 бита. Каждый из ключей вычис­ляется в соответствии с некоторой линейной функцией от блока исходного сообщенияи значения. Значение является линейной функцией от результата шифрования, бло­ка исходного сообщенияи значения. После вычисления значения для последовательности блоков применяют еще два шага вычисления согласно формуле:

где Ζ — сумма по модулю два всех блоков сообщения, a L — длина сообщения.

2.       Требования к применяемым в криптографии хэш-функциям

Анализ условий применения функций хэширования и практического их использования позволил сформулировать требования, предъявляемые к применяемым в криптографии бесключевым хэш-функциям. Они состоят в следующем:

3.        Стойкость к вычислению прообраза – невозможность нахождения неизвестного прообраза для любых предварительно заданных хэш-значений, т.е. для заданной хэш-функции  вычислительно невозможно найти неизвестный прообраз  при предварительно заданном хэш-значении  для любого значения . Под термином “вычислительно невозможно” здесь и далее будем понимать, что алгоритм, выполняющий данное преобразование, обладает не менее чем экспоненциальной сложностью.

4.        Стойкость к вычислению второго прообраза – невозможность нахождения любого другого прообраза, который давал бы такое же хэш-значение, как и заданный, т.е. для заданной хэш-функции  и прообраза  вычислительно невозможно найти другой прообраз , для которого выполнялось бы условие .

5.        Стойкость к коллизиям – невозможность нахождения двух прообразов для которых вырабатывалось бы одинаковое значение, т.е. для заданной хэш-функции  вычислительно невозможно найти два прообраза  и , , для которых выполнялось бы условие .

Требование стойкости к коллизиям является более жестким, чем требование стойкости к вычислению второго прообраза, так как предполагает произвольный выбор двух прообразов.

Однонаправленной хэш-функцией называется функция , удовлетворяющая требованиям сжатия, простоты вычисления, стойкости к вычислению прообраза и стойкости к вычислению второго прообраза.

Бесколлизионной хэш-функцией называется функция , удовлетворяющая требованиям сжатия, простоты вычисления, стойкости к вычислению второго прообраза и стойкости к коллизиям.

На практике обычно используются хэш-функции, являющиеся одновременно бесколлизионными и однонаправленными.

Однонаправленные хэш-функции могут применяться для решения других задач, например, выработки ключей и псевдослучайных чисел. Для применения в таких задачах хэш-функция должна удовлетворять следующим требованиям [2]:

6.        Отсутствие корреляции – входные и выходные биты не должны коррелировать, т.е. изменение любого входного бита приводит к большим непредсказуемым изменениям выходных бит.

7.        Стойкость к близким коллизиям – для заданной однонаправленной функции  вычислительно невозможно найти два прообраза  и , для которых хэш-значения  и  отличались бы на малое количество бит.

8.        Стойкость к частичной однонаправленности – вычислительно невозможно восстановить любую часть входного сообщения так же, как и все сообщение. Более того, по любой известной части входного сообщения вычислительно невозможно восстановить оставшуюся часть (восстановление  неизвестных бит требует не менее чем  операций).

9.        Возможность работы в режиме растягивания – возможность вычисления хэш-функции при длине входного сообщения меньше чем длина хэш-значения.

Требование, предъявляемое к применяемым в криптографии хэш-функциям с секретным ключом, следующее:

вычислительная стойкость – невозможность нахождения хэш-значения для заданного сообщения без известного секретного ключа, т.е. для заданной ключевой хэш-функции  и одной или более корректных пар прообразов и хэш-значений  и неизвестном секретном ключе  вычислительно невозможно найти другую корректную пару  для любого .

Требование вычислительной стойкости предполагает выполнение требования стойкости ключа (по одной или более корректных пар прообразов и хэш-значения  вычислительно невозможно восстановить секретный ключ ), однако, требование стойкости ключа не предполагает выполнение требования вычислительной стойкости.

Функция хэширования с секретным ключом  является функцией выработки КАС, если выполняются требования сжатия, вычислительной простоты (при известном сеансовом ключе) и вычислительной стойкости.

Следует различать функции выработки КАС и однонаправленные хэш-функции с секретным ключом, являющимся частью сообщения, так как они обладают различными свойствами. В функциях выработки КАС секретный ключ применяется к каждому блоку сообщения, а в однонаправленных хэш-функциях ключ используется префиксным (в начале сообщения), постфиксным (в конце сообщения) или комбинированным методом, что снижает стойкость функции.